Curse of Dimensionality: Volume Ratio

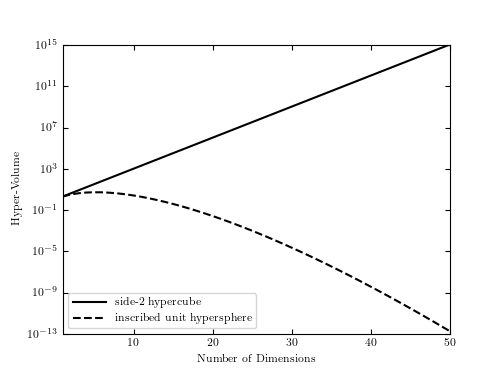
This figure shows the ratio of the volume of a unit hypercube to the volume of an inscribed hypersphere. The curse of dimensionality is illustrated in the fact that this ratio approaches zero as the number of dimensions approaches infinity.

Code output:

Python source code:

# Author: Jake VanderPlas
# License: BSD
#   The figure produced by this code is published in the textbook
#   "Statistics, Data Mining, and Machine Learning in Astronomy" (2013)
#   For more information, see http://astroML.github.com
#   To report a bug or issue, use the following forum:
#    https://groups.google.com/forum/#!forum/astroml-general
import numpy as np
from matplotlib import pyplot as plt
from scipy.special import gammaln

#----------------------------------------------------------------------
# This function adjusts matplotlib settings for a uniform feel in the textbook.
# Note that with usetex=True, fonts are rendered with LaTeX.  This may
# result in an error if LaTeX is not installed on your system.  In that case,
# you can set usetex to False.
from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)

dims = np.arange(1, 51)

# log of volume of a sphere with r = 1
log_V_sphere = (np.log(2) + 0.5 * dims * np.log(np.pi)
                - np.log(dims) - gammaln(0.5 * dims))

log_V_cube = dims * np.log(2)

# compute the log of f_k to avoid overflow errors
log_f_k = log_V_sphere - log_V_cube

fig, ax = plt.subplots(figsize=(5, 3.75))
ax.semilogy(dims, np.exp(log_V_cube), '-k',
            label='side-2 hypercube')
ax.semilogy(dims, np.exp(log_V_sphere), '--k',
            label='inscribed unit hypersphere')

ax.set_xlim(1, 50)
ax.set_ylim(1E-13, 1E15)

ax.set_xlabel('Number of Dimensions')
ax.set_ylabel('Hyper-Volume')
ax.legend(loc=3)

plt.show()

[download source: fig_volume_ratio.py]